Die Webseiten der Fachschaft Informatik am ERG Saalfeld

Zeitkomplexität

Erläuterung / Beschreibung
Landau-Notation
Beispiel: Ermittlung der Zeitkomplexität bei der Bestimmung von pythagoräischen Zahlentripel

experimentelle Ermittlung
Ermittlung durch theoretische Überlegungen

Berechnung des Zeitbedarfs mit Hilfe der Zeitkomplexität

1. Erläuterung / Beschreibung

Unter der Zeitkomplexität eines Problems wird in der Informatik die Anzahl der Rechenschritte verstanden, die ein optimaler Algorithmus zur Lösung dieses Problems benötigt, in Abhängigkeit von der Länge der Eingabe. Man spricht hier auch von der asymptotischen Laufzeit und meint damit, in Anlehnung an eine Asymptote, das Zeitverhalten des Algorithmus für eine potenziell unendlich große Eingabemenge. Es interessiert also nicht der Zeitaufwand eines konkreten Programms auf einem bestimmten Computer, sondern viel mehr, wie der Zeitbedarf wächst, wenn mehr Daten zu verarbeiten sind, also z. B. ob sich der Aufwand für die doppelte Datenmenge verdoppelt oder quadriert (Skalierbarkeit).

2. Landau-Notation

Da es sich bei uns in erster Linie um Algorithmen und nicht um Funktionen handelt, wird bei uns die Zeitkomplexität so geschrieben (Beispiele):
  O(n)             - für lineare Suche
  O(n²)            - Sortieren mit Bubble- bzw. Selectionsort
  O(n log n)       - Sortieren mit Quick- oder Mergesort

3. Beispiel: Ermittlung der Zeitkomplexität bei der Bestimmung von pythagoräischen Zahlentripel

Es soll hier exemplarisch die Zeitkomplexität zur Bestimmung von pythagoräischen Zahlentripel einmal "experimentell" (hier gemeint als Ausführen eines Programms mit verschiedenen Grenzen und Messung der zugehöringen Zeit. Außerdem soll die Zeitkomplexität durch Überlegung ermittelt werden, also theoretisch.'

a) experimentelle Ermittlung

Dazu wird folgendes Programm verwendet:
use strict;
use warnings;

my $grenze = $ARGV[0];

for (my $a = 1; $a < $grenze; $a++) {
  for (my $b = $a; $b < $grenze; $b++) {
    for (my $c = 1; $c < 2*$grenze; $c++) {
          if ($c**2 == $a**2 + $b**2) {
            print " $a \t $b \t $c \n";
      }
    }
  }
}
Der Aufruf sah bei mir so aus:

Es geht ja darum, für verschiedene Grenzen (also Zahlen, bis zu denen pythagoräische Zahlentripel gesucht werden sollen) die Zeiten zu ermitteln. Dazu ändern wir das Programm so ab:
use strict;
use warnings;

my $grenze = $ARGV[0];
my $anfang = time();    # Anzahl der Sekunden seit  1.1.1970  0.00 Uhr

for (my $a = 1; $a < $grenze; $a++) {
  for (my $b = $a; $b < $grenze; $b++) {
    for (my $c = 1; $c < 2*$grenze; $c++) {
          if ($c**2 == $a**2 + $b**2) {
            #print " $a \t $b \t $c \n";
      }
    }
  }
}

my $ende   = time();    # Anzahl der Sekunden seit  1.1.1970  0.00 Uhr
my $dauer  = $ende - $anfang;   # Anzahl der Sekunden für das Programm
print "Dauer: ${dauer}s \n";
Der Aufruf sah bei mir so aus:

Es ergibt sich damit folgende Wertetabelle:

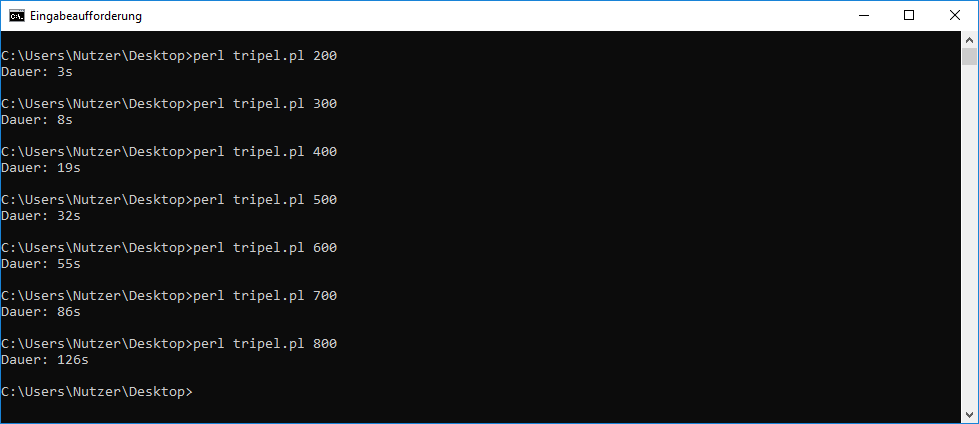
Grenze n 200 300 400 500 600 700 800

Zeit t in Sekunden 3 8 19 32 55 86 126

Im Diagramm sieht das so aus:

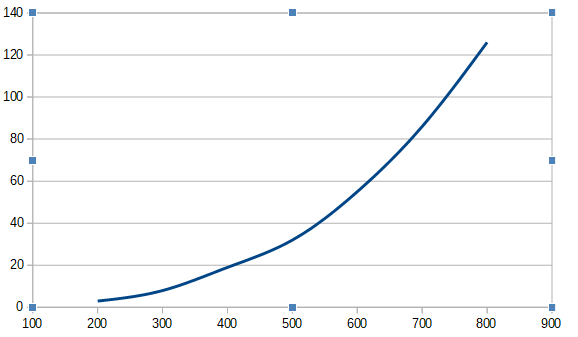
Damit läßt sich für den Zusammenhang zwischen n und t eine Potenzfunktion vermuten, z.B. t(n) ~ n² oder t(n) ~ n³ oder, oder, oder?
Dazu untersuchen wir die unsere Werte aus der Tabelle auf entsprechende Quotienten:

Grenze n 200 300 400 500 600 700 800

Zeit t in Sekunden 3 8 19 32 55 86 126

n² / t 13.333 11.250 8.421 7.812 6.545 5.697 5.079

n³ / t 2.666.666 3.375.000 3.368.421 3.906.250 3.927.272 3.988.372 4.063.492

Man erkennt deutlich, dass für n² / t der Quotient nichtmal annähernd konstant ist. Bei n³ / t scheint sich der Quotient bei 4.000.000 einzupegeln. Um das genauer zu verifizieren, habe ich zusätzlich die Zeiten für n = 1000 und n = 2000 bestimmt. Damit ergibt sich folgende Tabelle.

Grenze n 200 300 400 500 600 700 800 1000 2000

Zeit t in Sekunden 3 8 19 32 55 86 126 232 1865

n³ / t 2.666.666 3.375.000 3.368.421 3.906.250 3.927.272 3.988.372 4.063.492 4.310.344 4.289.544

Damit ist hinreichend genau bestätigt, dass für diesen Algorithmus n³ / t = constant gilt und damit t ~ n³ oder O(n³).

b) Ermittlung durch theoretische Überlegungen

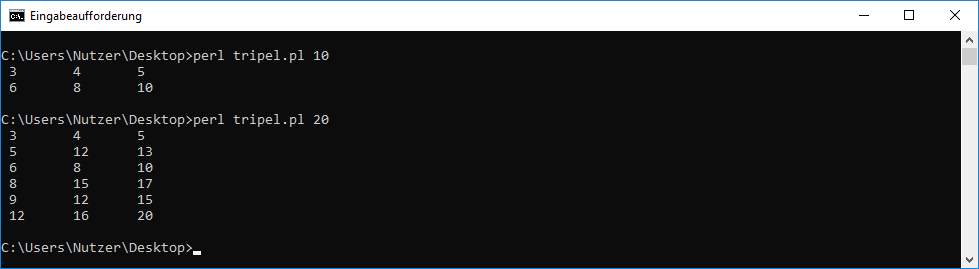
Wir betrachten jetzt das Programm mit 2 (kleinen) Änderungen:
use strict;
use warnings;

my $grenze = $ARGV[0];

for (my $a = 1; $a < $grenze; $a++) {
  for (my $b = 1; $b < $grenze; $b++) {
    for (my $c = 1; $c < $grenze; $c++) {
          if ($c**2 == $a**2 + $b**2) {
            print " $a \t $b \t $c \n";
      }
    }
  }
}
Hierbei wurde im Vergleich zur Ausgangsvariante Folgendes geändert:
1. Die innere Schleife läuft nur noch von 1 bis zu $grenze. Das bedeutet, diese Schleife läuft nur noch halb so lange.
2. Die zweite Schleife (also die mit $b) beginnt jetzt auch mit 1 und nicht mehr bei $a. Das bedeutet, diese läuft jetzt im Schnitt doppelt so lang.
Das bedeutet, dass durch die Änderung der inneren Schleife sich die Anzahl der Aufrufe für die if-Anweisung im Vergleich zur 1. Version halbiert und durch die 2. Änderung sich die Anzahl der Aufrufe für die if-Anweisung wieder verdoppelt. Das bedeutet, die beiden Änderungen heben sich in Hinblick auf den Zeitbedarf gegenseitig auf.

Um jetzt die Zeitkomplexität zu ermitteln gehen wir davon aus, dass als Parameter eine Zahl eingegeben wird, die wir jetzt n nennen.
Dann wird die äußere Schleife (also die mit $a) n-mal durchlaufen bzw. wird die Schleife mit $b n-mal aufgerufen.
Die zweite Schleife (also die mit $b) wird auch n-mal durchlaufen bzw. wird die Schleife mit $c n-mal aufgerufen.
Die dritte Schleife (also die mit $c) wird auch n-mal durchlaufen bzw. wird die if-Anweisung n-mal aufgerufen.
Insgesamt wird als die if-Anweisung n * n * n oder n³ -mal aufgerufen. Da die Zeit für die if-Anweisung als konstant betrachtet werden kann, erhalten wir durch diese Überlegungen t ~ n³ oder O(n³).

4. Berechnung des Zeitbedarfs mit Hilfe der Zeitkomplexität

Das Programm für die pythagoräischen Zahlentripel wird auf einen alten Computer gestartet. Als Parameter wird 600 eingegeben. Da dieser Rechner schon etwas betagt ist, braucht er dafür 80s. Es soll jetzt berechnet werden, wie lange der Computer braucht, wenn als Parameter 3000 eingegeben wird.

Gegeben ist: n₁ = 600, n₂ = 3000 das bedeutet, die Anzahl für n hat sich verfünffacht.

wegen O(n³) bzw. t ~ n³ bedeutet das, dass die Zeit t₂ das 125-fache des alten Wertes t₁ ist (5³ = 125).

Damit ist t₂ das 125-fache von 80s gleich 10.000s! (Das sind rund 167 Minuten oder 2 Std. 47 min.)

Weblinks

Zeitkomplexität (Wikipedia)
Landau-Symbole (Wikipedia)
Funktionen für Datum und Uhrzeit (SelfHTML Version 8.1.1)

zurück