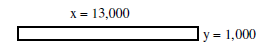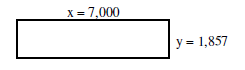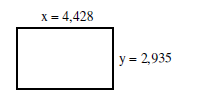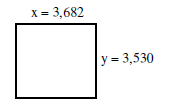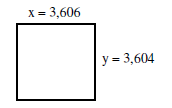Die Webseiten der Fachschaft Informatik am ERG Saalfeld

Heron-Verfahren

Das Heron-Verfahren, Heronsche Näherungsverfahren oder babylonische Wurzelziehen ist ein Verfahren zur Berechnung der Quadratwurzel einer (positiven) Zahl.

Die Idee hinter diesem Verfahren beruht darauf, ein Rechteck in ein flächengleiches Quadrat umzuwandeln. Die Seitenlänge dieses Quadrates ist dann die Wurzel aus der Fläche des gegebenen Rechtecks. Dieses Verfahren soll jetzt am Beispiel von Wurzel 13 demonstriert werden.
 

Wir wählen uns ein Rechteck mit den Seiten x=13 und y=1. Dieses Rechteck hat die Fläche A=13. Wenn wir daraus ein flächengleiches Quadrat erstellen, dann hat das auch die Fläche 13 und die Seitenlänge ist Wurzel(13).
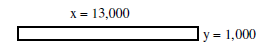Um die Fläche dem Quadrat anzunähern, bestimmen wir den Mittelwert der beiden alten Seitenlängen. Es ergibt sich x = (13 + 1) / 2 = 7. Für die andere Seite ergibt sich y = A / x = 13 / 7 = 1,857 .
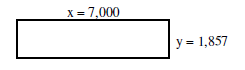Um das Rechteck noch weiter dem Quadrat anzunähern, bilden wir für die erste Seite wieder den Mittelwert aus den beiden Seiten. Es ergibt sich x = (7 + 1,857) / 2 = 4,428. Für die andere Seite ergibt sich y = A / x = 13 / 4,428 = 2,935 .
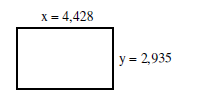Um das Rechteck noch weiter dem Quadrat anzunähern, bilden wir für die erste Seite wieder den Mittelwert aus den beiden Seiten. Es ergibt sich x = (4,428 + 2,935) / 2 = 3,682. Für die andere Seite ergibt sich y = A / x = 13 / 3,682 = 3,530 .
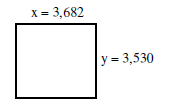Wir führen diesen Schritt nocheinmal aus (wird genau genug). Es ergibt sich nun x = (3,682 + 3,530) / 2 = 3,606. Für die andere Seite ergibt sich y = A / x = 13 / 3,606 = 3,604 .
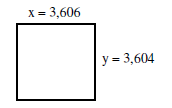Unsere Seiten x = 3,606  und  y = 3,604 haben einen Unterschied von 0,002. Wir wollten die Wurzel auf 2 Stellen nach dem Komma genau. Das ist damit erreicht.

Aufgabe

Erstellen Sie ein Programm, welches für Wurzel aus 5 einen Näherungswert nach dem Heronverfahren ermittelt. Dieser Näherungswert von Wurzel 5 soll auf 2 Stellen nach dem Komma genau sein. Das Programm soll nur das Ergebnis ausgeben.

Bei mir sah der Aufruf so aus:

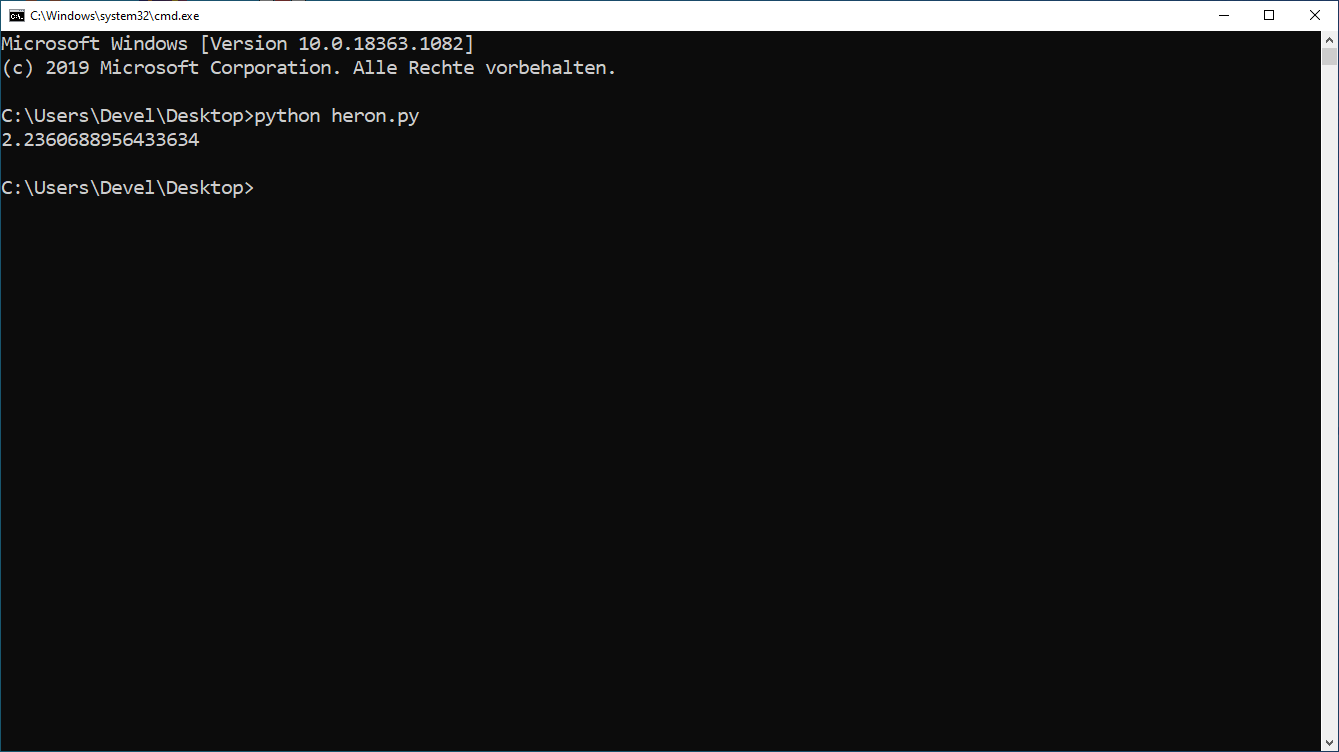
Aufgaben

1. Bringen Sie das Programm zum Laufen.
2. Überprüfen Sie das Ergebnis z.B. mit einem Taschenrechner.
3. Erklären Sie, woher der Unterschied kommt.
4. Ändern Sie das Programm so ab, dass hier kein Fehler suggeriert wird.
5. Ändern Sie das Programm so ab, dass man die Zahl, von der die Wurzel bestimmt werden soll, als Parameter übergibt.
6. Ergänzen Sie das Programm um eine Überschrift (unterstrichen, Leerzeile, usw.).
7. Erstellen Sie zu Ihrem Programm ein Struktogramm.
8. Informieren Sie sich über Heron von Alexandria (siehe Weblinks)

Weblinks

1. Wikipedia: Geometrische Veranschaulichung des Heron-Verfahrens
2. Wikipedia: Heron von Alexandria
3. Wikipedia: Heronsball
4. Wikipedia: Satz des Heron (Dreiecksberechnung)
5. Wikipedia: Heronsbrunnen

zurück