Die Webseiten der Fachschaft Informatik am ERG Saalfeld

Binomialkoeffizient

Aus der 8. Klasse sind die binomischen Formel und damit vielleicht auch das Pascalsche Dreieck bekannt. Aus der 10. Klasse ist die Binomialverteilung und damit auch der Begriff Binomialkoeffizient bekannt. Um den Binomialkoeffizient rekursiv definieren zu können, sollen diese Begriffe hier nochmal wiederholt werden.

 (a+b)0 =                   1                                                                                   1
 (a+b)1 =               a   +   b                                                                            1      1
 (a+b)2 =            a2 +  2ab  +  b2                                                                     1     2      1
 (a+b)3 =        a3  + 3a2b  + 3ab2  +  b3                                      =>                      1     3      3     1
 (a+b)4 =    a4  + 4a3b +  6a2b2 +  4ab3 +  b4                                                       1     4     6      4     1
 (a+b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5                                                  1     5    10     10     5     1

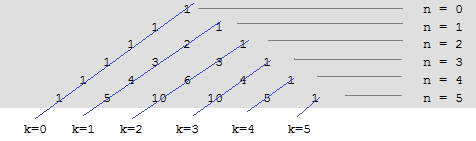
In diesem PASCALschem Dreieck werden die Zeilen und Spalten wie im folgenden Bild nummeriert:

Beispiel: für n=4 ist das 3. Element (also k=2, denn Zählung beginnt mit 0!) die 6 das schreibt man in der Mathematik so:

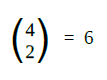
Man erkennt im PASCALschen Dreieck leicht, dass sich eine Zahl (außer am Rand) als Summe der beiden Zahlen genau darüber, also in der darüberliegenden Zeile ergeben, z.B. 10 = 4 + 6 oder 3 = 1 + 2. Außerdem ist der Rand, also k=0 oder k=n, immer 1. Damit ergibt sich allgemein:

Definition

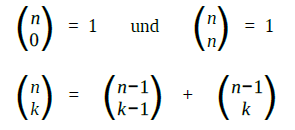
Diese Definition schreiben wir in Hinblick auf die zeilenweise Eingabe für den Computer so:

 bin(n,0) = 1    und    bin(n,n) = 1
 bin(n,k) = bin(n-1,k-1) + bin(n-1,k)

Programm

def binominalkoeffizient(n,k):
  if (k==0) or (k==n):
      rueckgabe = 1
  else:
      rueckgabe = binominalkoeffizient(n-1,k-1) + binominalkoeffizient(n-1,k)
  return rueckgabe

print(binominalkoeffizient(4,2))

Der Aufruf sah bei mir so aus:

Aufgaben

1. Bringen Sie das Programm zum Laufen.
2. Testen Sie das Programm mit anderen Zahlen.
3. Ändern Sie das Programm so ab, dass die Zahlen als Parameter übergeben werden.
4. Ergänzen Sie das Programm um eine Überschrift (unterstrichen, danach Leerzeile).
5. Ändern Sie das Programm so ab, dass die Ausgabe so erfolgt (hier für Parameter 4 und 2): "binominalkoeffizient(4,2) = 6"

zurück