Die Webseiten der Fachschaft Informatik am ERG Saalfeld
Sieb des Eratosthenes
Anmerkung: Das Sieb des Eratosthenes gilt als der älteste bekannte Algorithmus.
Siehe dazu auch den Artikel in der Wikipedia
Suchen der Primzahlen per Hand bis 30
| 1. Schritt: schreibe alle Zahlen bis 30 auf |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
| 2. Schritt: erste Primzahl ist die 2 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
| 3. Schritt: streiche alle Vielfachen |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
| 4. Schritt: suche die nächste Primzahl |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
| Wiederhole: streiche alle Vielfachen (siehe 3. Schritt) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
| suche die nächste Primzahl |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
| streiche alle Vielfachen |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
Anmerkung: Man ist fertig mit dem "Sieben", wenn die aktuelle Primzahl größer ist als die Wurzel der oberen Grenze.
Hier in diesem Beispiel: die obere Grenze ist 30, die Wurzel daraus 5,477225575051661 - also braucht man für die 7 nicht mehr
weiterarbeiten => man kann aufhören (Abbruch).
Programm für die Primzahlen bis 100
feld = []
primzahl = 0
vielfaches = 0
def erstelle_feld():
#wir erzeugen ein Feld von 0 bis 99, im Feld ist die Feldnummer
for i in range(100):
feld.append(i)
def erste_primzahl():
#die erste primzahl ist 2
global primzahl
primzahl = 2
return primzahl
def streiche_vielfache():
#erstes Vielfaches ist 2*primzahl
global primzahl
vielfaches = 2 * primzahl
#die vielfachen der Primzahl werden durch 0 ersetzt (gestrichen)
while vielfaches < 100:
feld[vielfaches] = 0
vielfaches = vielfaches + primzahl
def suche_naechste_primzahl():
#primzahl um 1 vergroßern
global primzahl
primzahl = primzahl + 1
while feld[primzahl] == 0:
primzahl = primzahl + 1
def primzahlen_ausgeben():
for i in range (2,100):
if feld[i] != 0:
print(feld[i], end = ' ')
print('')
### Hauptprogramm ###
erstelle_feld()
erste_primzahl()
while primzahl < 10:
streiche_vielfache()
suche_naechste_primzahl()
primzahlen_ausgeben()
Das sah dann bei mir so aus:

Aufgaben
- Bringen Sie das Programm zum Laufen.
- Um Primzahlen z.B. in einem größeren Bereich zu bestimmen, müßte die "100" in diesem Programm an 3 Stellen geändert werden. Verwenden Sie eine Variable grenze.
- Damit die "10" in der 3. Zeile des Hauptprogramms nicht mehr angepasst werden muss, ersetzen Sie diese durch grenze**(0.5) .
- Testen Sie das Programm für verschiedene Bereiche. (Hier ist sicherlich grenze = 30 sinnvoll, denn die Ergebnisse stehen oben zur Verfügung!)
- Ergänzen Sie das Programm um eine Überschrift. Die soll unterstrichen werden, danach soll eine Leerzeile kommen.
- Unter der Ausgabe der Primzahlen soll die Anzahl der gefundenen Primzahlen angegeben werden.
- Für größere Bereiche soll wegen der Übersichtlichkeit in jeder Zeile 10 Primzahlen ausgegeben werden. (In der letzten Zeile die restlichen Primzahlen.)
- Es soll die Anzahl der Primzahlzwillinge ermittelt werden, also die Anzahl solcher Paare wie 3 - 5, 5 - 7, 11 - 13, 17 - 19.
- Auch die Primzahlzwillinge sollen ausgegeben werden (hier fordere ich kein bestimmtes Format, allerdings muss die Lösung erkennbar sein).
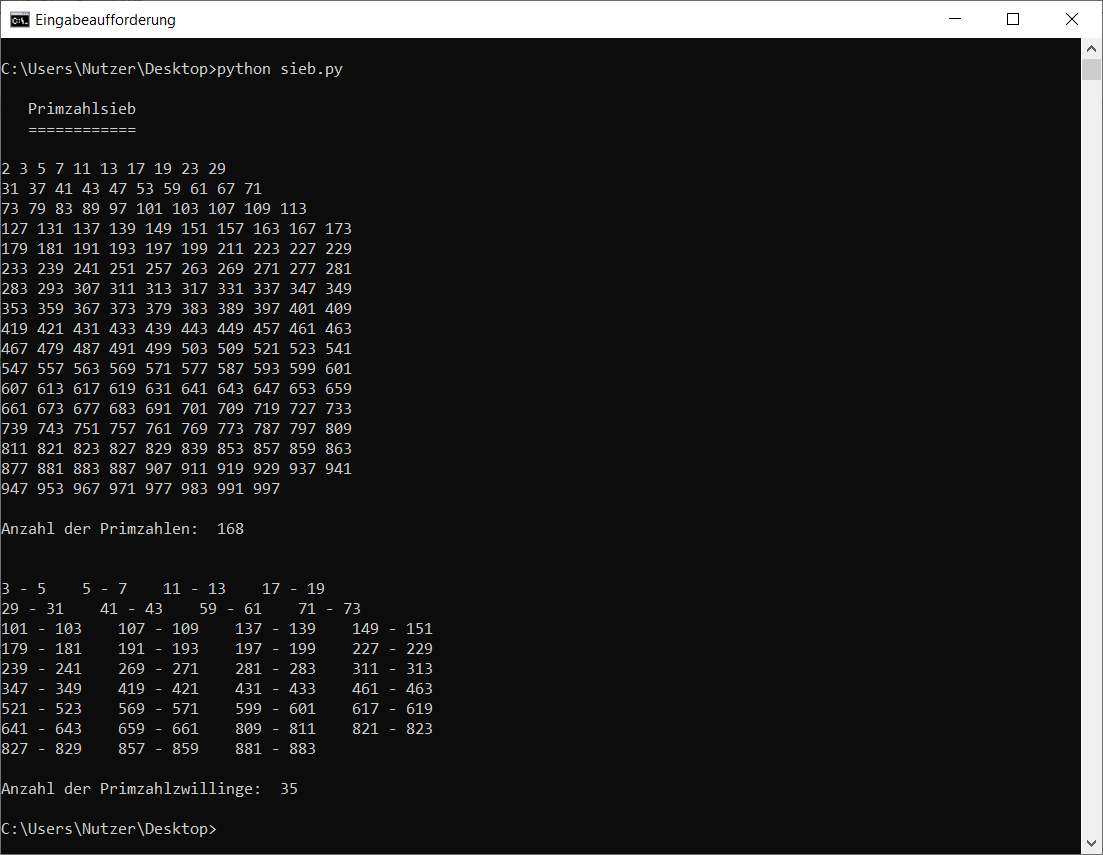
Für grenze = 1000 sah das bei mir so aus:
zurück
© ERG Saalfeld - HD. Kirmse + Dustin Wiese 14.08.2022
|

